第３信として「必ず役にたつ数検準１級体験記」にしたかったのですが、忙しさにかまけて書く機会を失ったまま今日まで来てしまい、記憶がだいぶ薄れてしまいました。「必ず役にたつ」というほどの資料を載せにくいのですが、「ままよ、恥かきのついでだ！」ということで今回も掲載します。インターネット上、数検準１級は、「これからがんばる宣言」ではない、実際の受験経過の記録がほとんどない中、何かの参考になればということでご容赦下さい。

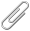さて、経過です。漢検や・英検の延長で受けてみたのです。実際には仕事の合間合間の作業な上、英検や漢検やＴＯＥＩＣやと、ごちゃごちゃしたスケジュールをかいくぐっての受験でしたので、途中それなりの苦労があり、やはり２級と準１級受験は大変でした。

まず中３相当の３級からです。これはさすがに問題ありませんでした。とはいえ、一次で２題ミスし、二次試験の作図が一題書けませんでした。おそらく周りの中３の若者も同じかと想像しながら時間切れまで悪戦苦闘しました。時間切れになったときのくやしかったこと！

準２級は思いの外簡単でした。受験前に三角比の公式集のみ見直した記憶があります。驚いたことにほとんど受験時の記憶がありません。２次の最後のいわゆる「数検問題」だけは善し悪しは別として変わったタイプの問題だなーと感じていた記憶があります。残っている問題を引っ張り出しましたら、１次は３８分で終わり、２次はメモに「見直しまでで６０分」と記してありました（２次の検定時間は当時１２０分。今は９０分です）。

２級、忘れていることだらけで苦労しました。数検の一次は「努力すれば必ず解ける」典型問題のみですから、いいですね。数学が好きという人の大半は実は計算が好きなのですから、そういう普通の計算好きにはたまらくうれしいテストです。とはいえ、私の場合公式からしてすっかり忘れていました。ご存じの通り、この数�Uと数Ｂの範囲はかなり広く、やり直しのための時間が思ったほどなく、あせりました。ここで迷いました。本当は忘れているのだから本格的に教科書に戻るべきですが、「数�U・Ｂだからなー、いいや」という少し安易な気持ちのまま本屋に行き、ひさしぶりに高校参考書コーナーを渉猟しました。結果、一連の「マセマ」のシリーズを使うことにしました。かっこつけずにメネラウスの定理では「行って、戻って、行って、行って、中に切り込む」。三角関数の加法定理では「サイタ、コスモス、コスモス、サイタ」のような暗記をしました。割り切るとこのシリーズはとてもよくできています。大いに参考にさせていただきました。感謝。三角関数などがいい例ですが、公式が多すぎるのが数�U・Ｂの特徴なのですから、いたしかたないですね。遙か昔、高校生時代、生意気だった私はここをしくじりました。くだらない暗記などするものかというような馬鹿な自信、今思えば赤面の限りです。どの学習もそうですが、見せかけの馬鹿馬鹿しさを嫌う余りの失敗でした。公式はいざとなれば自分で作るというのは理想ですが残念、そこまでゆっくり解く時間がありません。今回の２級のやり直しは結局、公式はマセマ。作業は過去問でと決め、学習しました。

これに対し２次は考える問題です。本当の数学好きな人は心底楽しめると思います。そういう人で大学受験で数�Uと数Ｂをとっていれば何も問題なくできるはずです。ただし私の場合現役ではありませんので事情は大違いでした。「昔取った杵柄」「年寄りの冷や水」「運動会のお父さんの駆けっこ」、後何と言えばいいでしょう・・・一回目はまったくだめでした。言ってみれば偵察に行ったようなものでした。最初の受験時、過去問集の１冊目の半分も終わるかどうかでした。これでは傾向すらつかめず２次は惨敗。

結果、２級の第一回の受験は１次のみ合格。もちろん数検独特の制度、「１次もしくは２次のみの合格は次回以降申請すれば永久免除」の特権があることを利用することにしました。

２度目の２級受験、相変わらず過去問集を解きました。この時期、数検発行の過去問集が差し替えの時期で、ほとんど同タイプの旧版と新版で問題集が２冊使えました。時間が余りとれなかったせいか、解き終わったときの達成感がないまま、まあ、２冊終わったかな、というところで受験。結果予想外にいい成績で受かりました。

受かったのですが、学習の仕方がやっつけ仕事だったという失敗感が残りました。挑戦し始めたころは、数検の準１級ばかりははるか遠くの課題で、現状との距離感がありすぎ、考えてもいませんでした。２級に受かってようやく次もひょっとして・・・という気持ちが芽生えました。

２００４年当時は準１級でも問題の一部に数�Tや数�Uの範囲も出題されましたのでいざとなればそのタイプの問題を選択すれば２次は何とか・・・・とも考えていました。つまり一次さえ突破できればクリアできるかもしれないと考えました。

とはいえ、さすがに気が重かったです。高校時代以来の何十年ぶりの数�Vです。本当にかすかな記憶しかありませんでした。言ってみれば一大決心をしました。２級での失敗にこり、教科書を買ってきて、教科書レーダーも買ってきて、本気で最初から解き直すことにしたのです。教科書レーダーを使うのは自分では生まれて初めてです。ノートもルーズリーフ形式ですが新しく購入。まなじりを決して始めたのです。

現役の高校生にどうかはわかりませんが、自学自習の私には教科書＋教科書レーダーのセットが学校と先生の代わりの役割をしてくれました。教科書はやはりそれなりにいいものです。生意気な言い方をしますが、数学世界の大きな流れの中での役割分担をしたものが教科書ですから、一字一句に気配りがあります。どんな表現も意味があります。例えば自然対数の底ｅの導入式・説明の仕方に２種類あるのもそれなりの意味があるのだろうと推察できます。参考書や問題集はこの種のニュアンスが行間にありません。答えや導き方はあっても説明の苦しみ（時にはごまかし）がないとでもいえばいいのでしょうね。こちらも腰を据えて教科書を見ているせいで、数�Vは結構行間が楽しめました。人に言うほどのことではないのですが、理屈がわかることが本当にうれしい！ただし答えがないのが欠点。そこで本来は数学が苦手な生徒さんの友、教科書レーダーが大活躍した次第です。

本屋の棚を探している時に一つ大発見がありました。ブルーバックスの棚で見つけた「グレープス」というグラフ作製ソフトの存在です。いやーこの公開ソフトはよかったです。今まで計算はできてもそのグラフのイメージがまったくつかめなかった式がグラフ化されるのです。ありがたかったです。はるか何十年前にこのソフトを知っていたら、私の人生は変わっていただろうとすら思いました。複雑な式⁽¹⁾をイメージ出来る人もいるのかもしれませんが、私にはまったく無理なわけで、この種の式のグラフ化が可能なのですからすごい。画面やプリンターに出力されたときのうれしかったことといったらありませんでした。若い人、これを使わない手はないよ！あまりのうれしさに私は縮小してプリントアウトし、しばらく片端からノートにはりつけました。今もそのまま残っています。眺めるだけでもうれしくなります。この辺りの複雑な曲線、もう少しで現実世界の線描化が可能なのではないかという錯覚すら覚えます。これは高校生あたりの若い人には絶好です。数学は目に見えて楽しくなること間違いありません。とにかく私は夢中になりました。このソフトのせいで微分と積分にすっかりはまってしまい、教科書の微分積分のページが終わりかけたときには寂しさ（！？）すら覚えました。

行列は、私の時代には高校課程ではなかったため、今回初めて。ケーリーハミルトンの定理？次数を下げる？へーそうなんだあー・・・この語感うっとりしましたねー・・・何か頭よくなった気がしました。

そして最後に改めて気がつきました。ここまでを初等数学という人もいるのですね〜・・・初等ねー・・・やはりここが専門家との感覚の違いです！私にとっては、ここまでを「初等」と言われると本当に辛かったです。

トップページへ　　　次のページへ

(c) 2004-2014 必ず役に立つ体験記